Особенности построения рекурсии в программных продуктах 1С

Определение рекурсии в программировании

Рекурсия в программировании — это возможность дать определение функции, используя в процессе саму определяемую функцию. В математике многие функции определены именно таким образом, поэтому и большинство языков программирования используют этот подход.

Итак, рекурсию используют, когда вычисление функции можно свести к её более простому вызову, а его – к еще более простому и так далее, пока значение не станет очевидно. Основное применение рекурсии нашли при работе с деревьями. В 1С это в основном работа с иерархическими справочниками.

Алгоритм сортировки массива при помощи бинарного дерева

Разбор начнем с двоичных (бинарных) деревьев. В таких деревьях каждый узел имеет не более двух потомков. Применений у них много, а алгоритм обхода будет примерно один для всех. Из каждого узла можно пойти либо налево, либо направо.

Для данного примера выберем алгоритм сортировки деревом. Он не оптимален по скорости и может служить только для демонстрации рекурсий.

Причем в общем случае в массиве могут быть не только числа. Если вы работаете с некоторым множеством значений, которым могут быть применены отношения тождества и порядка, то этот алгоритм применим и для них. Суть алгоритма очень проста. Нужно взять первый элемент массива и сделать его корнем дерева. Затем выполняем простую операцию.
Если второй элемент массива больше значения в корне, делаем его правым листом. Если меньше, левым.

С остальными элементами поступаем так:

● если он больше или равен текущему узлу, то идем вправо по дереву;
● если меньше, то влево.

После того, как достигли листа, придерживаемся следующего порядка:

● если число больше значения в листе – делаем его правым листом от текущего;
● если число меньше значения в листе – делаем его левым листом от текущего.

Так продолжаем до тех пор, пока не отсортируем все элементы массива. После этого наступает время собирать элементы в новый упорядоченный массив.

Реализация алгоритма построения двоичного дерева на языке 1С

Работу алгоритма построения дерева рассмотрим наглядно на примерах.

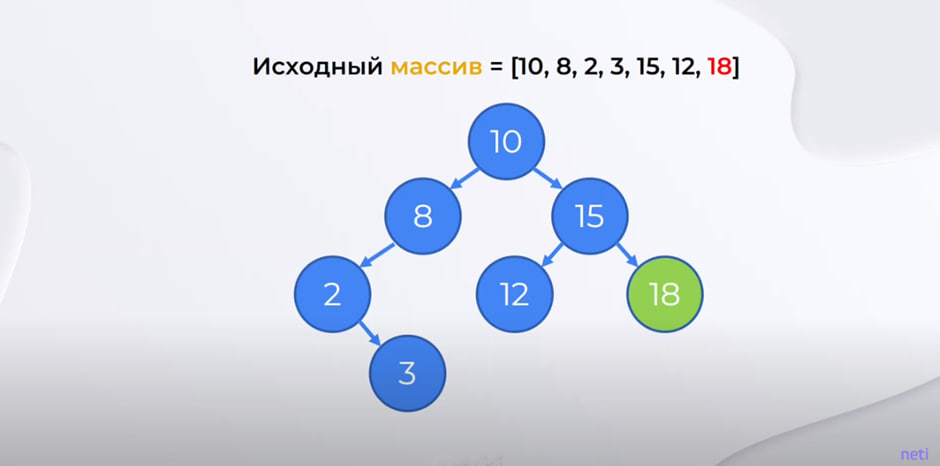
Пример 1. Пусть у нас имеется массив, представленный на рисунке ниже.

Берем первый элемент и делаем его корнем. Дальше сравниваем все элементы. 8 меньше 10, поэтому относим этот элемент к левому листу. 2 меньше 10 и меньше 8 – создаем левый лист от восьмерки. 3 меньше 10 и 8, но больше 2 – образуем правый лист от двойки. 15 больше 10 – это правый лист. 12 больше 10, но меньше 15 – это левый лист от 15. В итоге 18 больше всех элементов, поэтому создаем правый лист от 15.

Как это выглядит в коде представлено на изображении:

У процедуры построения дерева два параметра:

● текущий узел – это некоторый узел дерева, который мы обрабатываем в текущий момент;
● значение узла – это значение из массива, который мы сортируем.

Первое «Если» – это создание узла дерева:

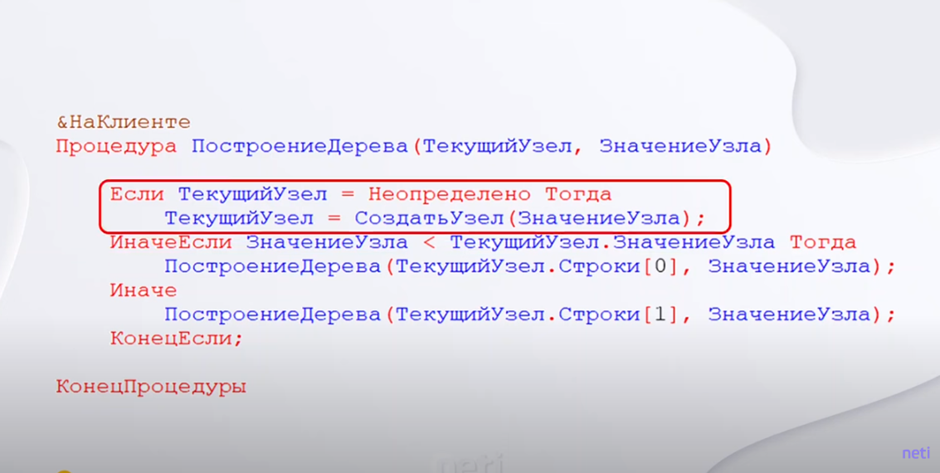
Второе «Если» – это переход к левому потомку:

«Иначе» – это переход к правому потомку.

При этом, обратить внимание нужно на следующее.

● Во-первых, для кода не имеет значение заполнено дерево или нет. Если оно пустое, то он создаст корневой элемент.
● Во-вторых, дерево не обходится полностью. Код движется от корня к листам по цепочке.
● В-третьих, для кода не важно есть ли у текущего узла левый или правый потомок: если есть, то он его обработает; если нет – создаст новый.

Теперь нам нужно все это собрать в упорядоченный массив.

Пример 2. Предположим, у нас есть дерево как на рисунке.

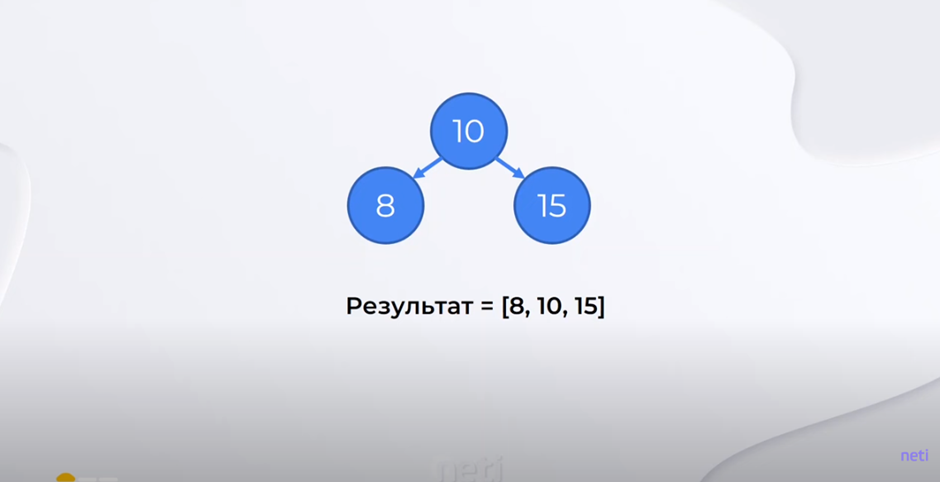
Применим следующую операцию. Левое и правое значения обернем в массив. Далее выполним операцию конкатенации левого массива, корня дерева и правого массива.

Если это только часть дерева, то полученный результат передадим на более высокий уровень.

Проверим работоспособность нашего алгоритма: если левого листа нет, то левый массив пустой, и мы получим правильный результат.

То же самое и с правым массивом: если слева результат обработки дальних потомков текущего узла, то все его значения меньше текущего, а значит результат будет верным. То же касается и правого поддерева.

Как наиболее удобно реализовать эту рабочую идею рассмотрим на следующем примере.

Пример 3. Нам нужно как можно скорее получить элементарное дерево, поэтому оптимально использовать рекурсию в глубину. Инициировать вычисление лучше в листах, а значит выбираем нисходящую рекурсию.

Рассмотрим одну особенность алгоритма.

Можно проверять наличие левого и правого потомков прямо в теле рекурсивной функции:

В этом случае придется писать оператор «Если» с четырьмя ветками.

Поэтому лучше передавать в рекурсивный вызов пустой узел и сделать этот случай терминальным. Тогда в теле функции остается всего лишь две альтернативы. Функция «Сформировать результат сортировки» имеет только один параметр – «Текущий узел», который содержит обрабатываемый узел дерева.

Если узла не существует, то она возвращает пустой массив. А если существует, то возвращает массив, который образуется конкатенацией левого поддерева, значения в узле и правого поддерева.

Особенности такого построения кода в том, что «красота требует жертв». В этом случае мы делаем в листе два лишних рекурсивных вызова с созданием пусть пустого, но массива (обрабатываем то, чего нет).

И если внутренний узел не имеет правого и левого потомка, то код также обработает пустой массив. Кажется, что это несущественно. Но представим, что в листе мы достигли максимальной глубины стека вызовов. Тогда при попытке обработки пустого узла мы получим падение клиента.

Также мы получаем некоторое количество действий, которые не добавляют к результату ничего ценного. И на них тратим процессорное время, что отрицательно сказывается на производительности.

Поэтому при переносе в продукт нужно решить: оставить код, который мы только что рассмотрели, или написать менее красивый, но более бережливый и надежный алгоритм, идею которого мы рассмотрели выше по тексту.

Пример 4. Перейдем к разбору деревьев, узлы которых могут иметь более двух потомков.

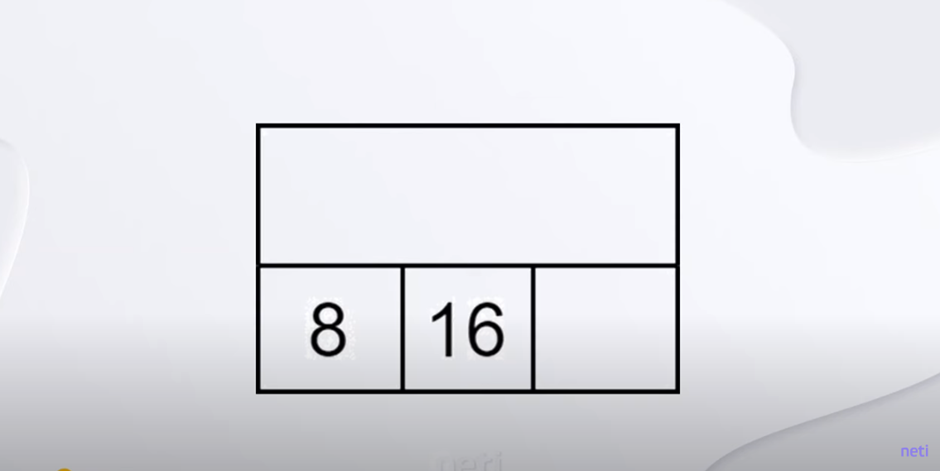
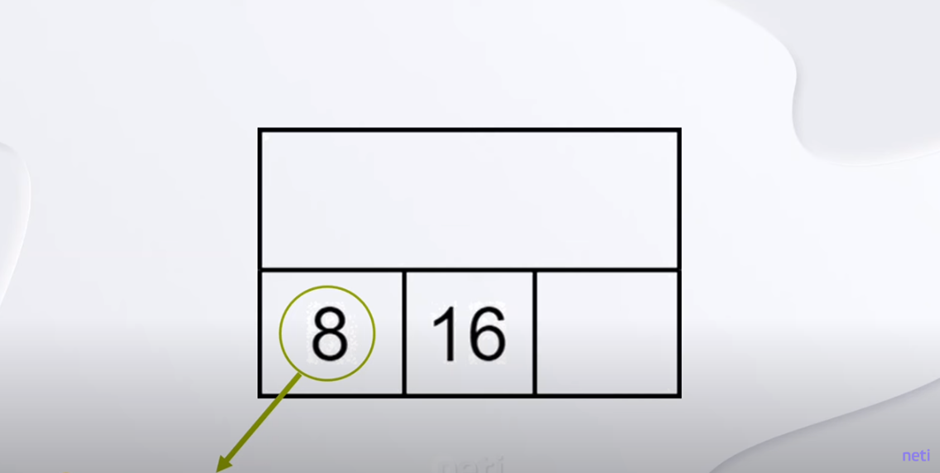
Предположим, что нам нужно реализовать поиск на B-дереве. Сам алгоритм очень прост. Как известно, узел B-дерева содержит ключи и ссылки на потомков. При этом количество ключей в узле всегда на единицу меньше, чем количество ссылок, кроме листовых узлов, которые не содержат ссылок вообще. Если нам нужно найти некоторое число в дереве, то действуем так. Берем корневой элемент и последовательно сравниваем его ключи с заданным значением.